Introduction
This document compiles the sound power and sound pressure levels as well as the frequency bands of BITZER compressors and is constantly being expanded. For further information, it is essential to read and observe the respective operating instructions!
The data was measured under laboratory conditions. For this purpose, the compressors stand freely on a solid foundation plate. The pipes are connected vibration-free as far as possible and fixed flexibly in the measuring chamber in such a way that the transmission of vibrations to the environment is largely excluded.
Real systems may show significant differences from the laboratory measurement: The airborne sound emitted by the compressor can be reflected by the surfaces of the system and thus increase the airborne sound level measured at the compressor. The vibrations of the compressor – depending on the damping of the mountings via the compressor feet and the piping – are also transmitted to the system and can excite other components there to such an extent that they contribute to the increase in airborne sound. If necessary, these transmissions can be minimised by suitable damping and fastening elements.
Unless otherwise stated, the determined power levels of the sound sources were created from sound intensity measurements according to ISO9614-2.
For the frequency bands in this document, sound power or sound pressure is measured at different frequencies:
- for octave bands in steps of twice the frequency in each case,
- for third octave bands, each octave band is further divided into 3 steps.
This data can be used, for example, to select suitable material for insulation.
Terms and units
The sound power (in watts) is the sound energy emitted by a sound source per unit of time. It is independent of the location of the sound source and the receiver or of the acoustic conditions of the room. It can be expressed as power in watts.
More common, however, is the corresponding logarithmic quantity: the sound power level.
The sound power level (in dB) is a measure of the sound power and proportional to it. Just like the sound power, the sound power level is independent of location.
The sound pressure (in Pa) refers to the effect of sound at a specific location – in this case the pressure fluctuations that the eardrum converts into movements for auditory perception. Like other pressures, sound pressure can be expressed in Pa, but here too the corresponding level is usually expressed as a logarithmic quantity in dB.
The sound pressure level (in dB) is a measure of sound pressure and is proportional to its square. Just like the sound pressure, the sound pressure level is location-dependent.
The decibel (dB) is not a physical quantity, but an auxiliary unit of measurement for a ratio of two quantities. The actual unit is called Bel (1 dB = 1/10 Bel) and denotes the decadic logarithm of the ratio of two similar quantities, e.g. levels. The unit is mainly used for quantities that change over orders of magnitude, such as sound power and sound pressure. If these quantities are represented as levels, the result is not only a numerically simpler representation: The human sensory impression runs approximately logarithmically to the intensity of the physical stimulus – thus the level of the acting physical quantity (sound power, sound pressure) approximately follows the human perception.
Level quantities can in principle assume both positive (dB > 0) and negative (dB < 0) values. At a level of 0 dB, the magnitude value would be equal to the reference value. For sound power and sound pressure, however, the reference values in the above formulae are so low (corresponding approximately to the lower human hearing threshold) that 0 dB or negative values are extremely rare in practice.
The unit dB(A) listed in this document denotes a weighted level that takes human perception into account – because the same sound pressure level is perceived in different loudness at different frequencies (pitches). In order to reproduce this hearing sensation, sound pressure levels are evaluated according to frequencies – with the A-weighting used here.
Calculation
The sound power level is calculated as the decadal logarithm of the ratio between the measured sound power and the reference value 10−12 W for airborne sound, multiplied by 10 (for unit dB instead of B).
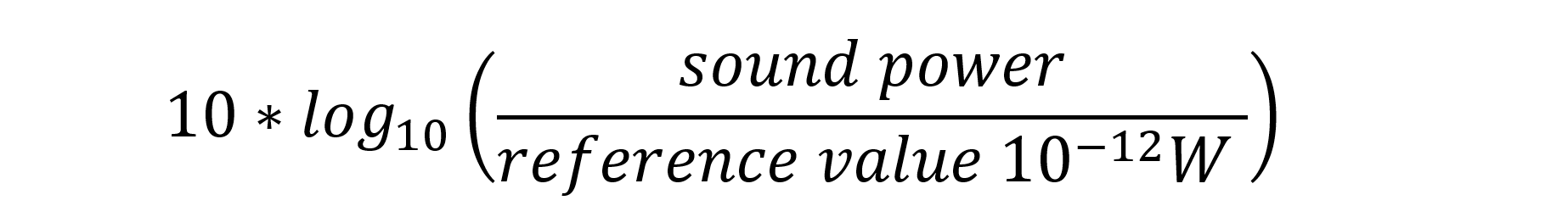
If the sound power is doubled and there are 2 identical sound sources, the sound power level increases by approx. 3 dB (= 10 * log10(2)).
The sound pressure level is calculated as the decadal logarithm of the ratio between the root mean square of the measured sound pressure and the squared reference value 2*10-5 Pa for airborne sound, multiplied by 10 (for unit dB instead of B).

If the sound pressure is doubled, the sound pressure level increases by approx. 6 dB (= 10 * log10(22) or 20 * log10(2)), provided the sound source is point-shaped and radiates evenly.
At ten times the sound pressure, the sound pressure level increases by 20 dB (20 * log10(10)).
When the distance is doubled, the sound pressure level decreases by approximately 6 dB, as the sound pressure decreases inversely proportional to the distance from the sound source.
The surface of the selected measuring surface and the reference surface are relevant for the conversion between sound power and sound pressure levels. The sound power level corresponds numerically to the sound pressure level that would be measured on a sphere with a surface area of 1 m2 if the sound source were a point in the center of this sphere. For free field conditions with hemispherical sound propagation at a distance of 1 m, the sound pressure level is approx. 8 dB below the sound power level.